题意简述
给你一个无向图,还有源点(S)和汇点(T)。求最少删除多少个点使得源点和汇点不连通。
点数n<=100,边数m<=600
思路框架
把每个点$u$拆成出点和入点,设为$Out(u)$和$In(u)$。
对于每个$u$,建流$In(u)\to_1 Out(u)$。
对于每个无向边,我们把它拆成两个有向边。
对于一条有向边$u\to v$,建流$Out(u)\to_{\infty}In(u)$
从$Out(S)$到$In(T)$跑最小割(最大流),就是答案了。
具体思路
这里讲讲我们是如何想到上面的拆点建图的。
原本我们的图是这样的:
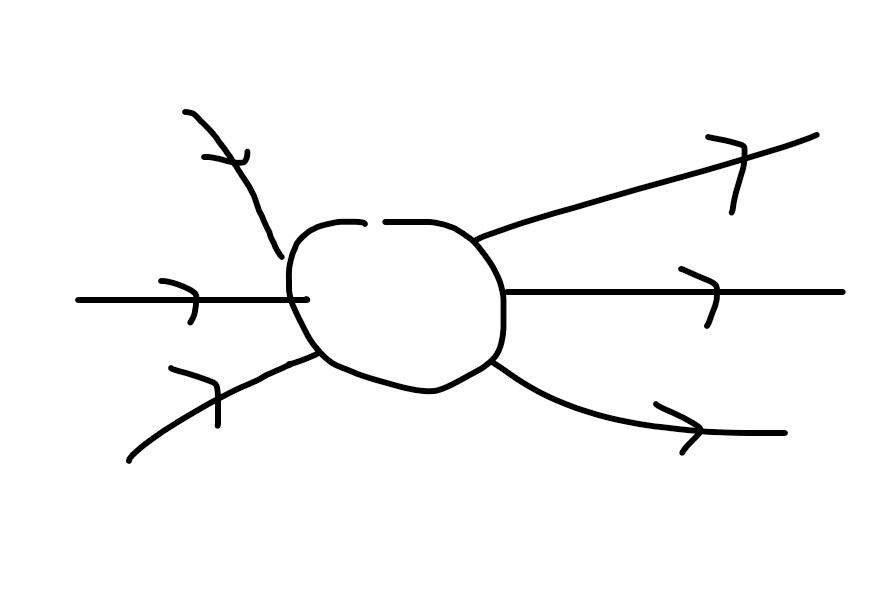
这是一个点,它有入边和出边。
变成这样: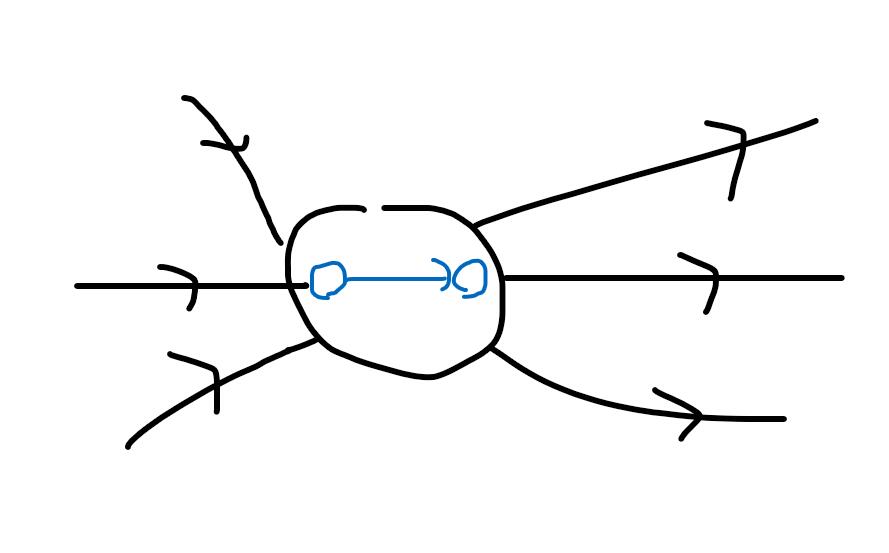
(蓝边流量为1,黑边流量为正无穷)
那么我们按照这样去建图,把一个点转化成一条边,删掉边就相当于删掉点。这样,我们就珂以把求最小割点的问题,转化成求最小割边的问题了。
然后由于原图上,我们只能删除点,不能删除边。我们只要把原图上的边权都变成无穷大,就不会割掉原边了(显然不是最优解啊)。
然后,由最小割=最大流,跑一遍Dinic就完了。
代码
1 |
|