由于作者水平就只能到模板,所以笔记也就写到这里。
FFT
简介
FFT是干啥的?它是用来加速多项式乘法的。我们平时经常求多项式乘法,比如$(x+1)(x+3)=(x^2+4x+3)$。假设两个式子都是$n$项(不足的补0),那朴素的算法是$O(n^2)$的。
那么,我们能做到$O(nlogn)$做么?
你也许觉得不珂能。的确,不看题解,是很难自己想到正解的(除非你是欧拉费马级别的天才)
前置知识
多项式点值表示
我们平常表达多项式,都是用系数表达的。当然,还有点值表达。用平面直角坐标系上的$n$个点,唯一确定一个(不超过)$n-1$次的多项式。它的一个特殊形式,就是两点确定一条直线。
点值转系数表达,你只需要解一个方程组就珂以了。(高斯消元,这样是$O(n^3)$的)
复数
复数的定义
这个很多人知道。定义$i=\sqrt{-1}$,即虚数单位。形如$a+bi$的数就是复数(complex)。
复数$a+bi$的辐角:从$(0,0)$到$(a,b)$的线段和$x$轴的夹角。这个夹角,是顺时针方向的夹角。取值范围是$[0,360]$。
复数的几何意义
在一维数轴上,我们把一个数乘以$-1$,相当于旋转了$180$。
那么,我们把一个数乘以$\sqrt{-1}$,相当于:乘两次是旋转$180$。所以,乘一次就是旋转$90$,也就是竖起来了。“竖起来”,这个概念很好表示,就是$y$坐标。
那么,$a+bi$就相当于平面直角坐标系上的点$(a,b)$。当然,你也珂以把它看成一个向量,从$(0,0)$到$(a,b)$。
复数的运算
复数的加法:$(a_1+b_1i)+(a_2+b_2i)=(a_1+a_2)+(b_1+b_2)i$。(这样也就包含了减法的情况)
复数的乘法:$(a_1+b_1i)\times (a_2+b_2i)$
我们把括号拆开,然后把$i^2$都变成$-1$(由$i$的定义)。易得,它等于:$(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i$
(n次)单位复根
满足$x^n=1$的所有复数解中,辐角最小且不为$0$的那个复数。记作$w_n$。不难发现,所有满足条件的$x$,用向量表示后,把单位圆$n$等分。
举个栗子,$n=6$的时候,解的分布是这样的: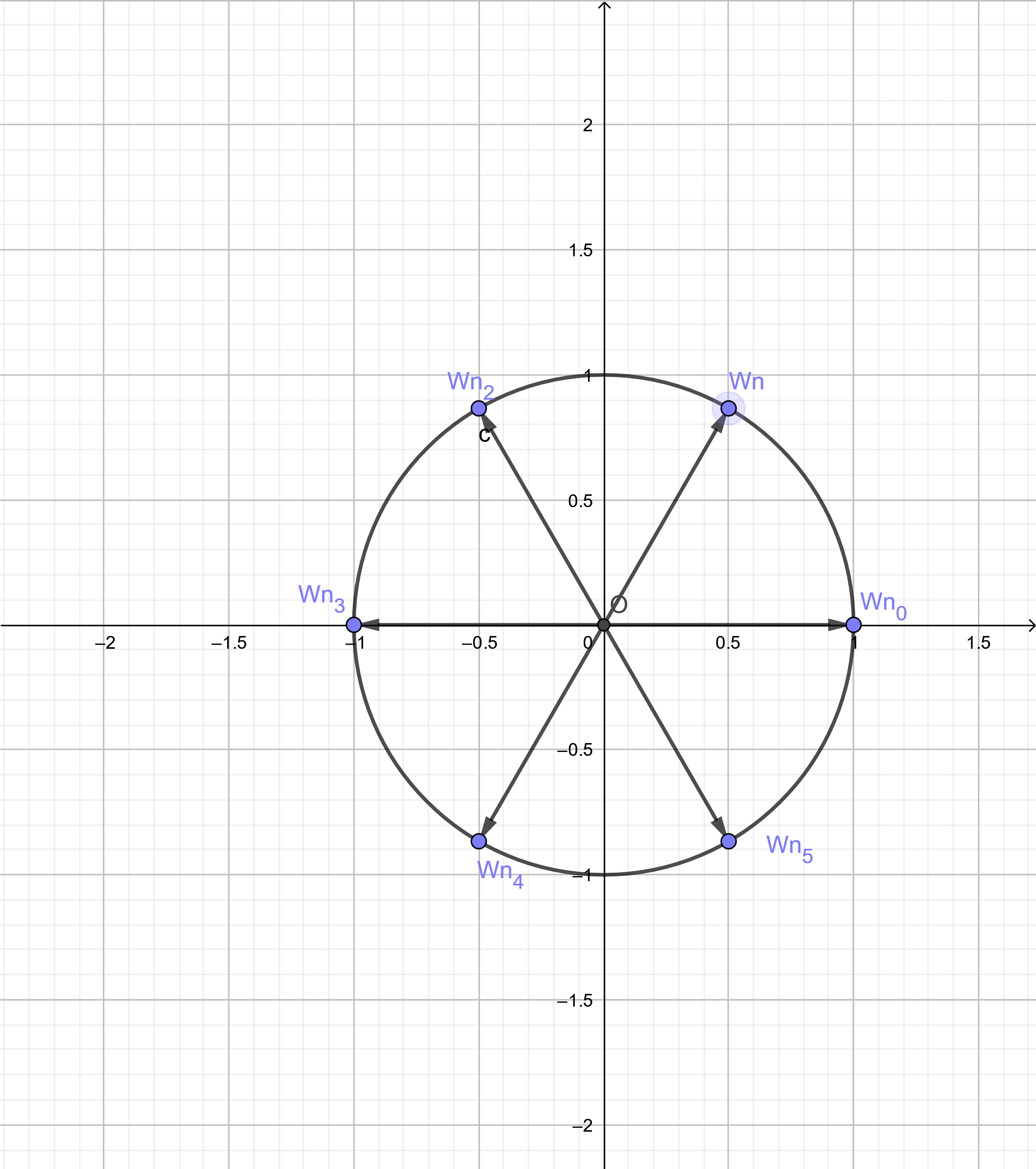
其中,$\omega n$就是图中标出来的,辐角大于0且最小的那个向量。
单位复根的性质
- $w_{2n}^{2k}=w_{n}^{k}$(珂以把$w_n^k$看成是$360\deg\times \dfrac{k}{n}$,这条证毕)
- $w_n^{k+n/2}=-w_n^k$。(这里$n/2$不取整,就是小数) (把$n/2$看成是转半圈,转半圈也就是$x,y$坐标都变负,这条也证毕)
正式开始!
上面不是说了点值表示么。对于两个用点值表示的多项式,只要把对应的点值乘起来即珂。
但是,我们要取$n$个点(DFT),每次$O(n)$求值,不是要$O(n^2)$了么?
而且,把点值转换成系数(插值,IDFT)的过程,不是要$O(n^3)$么?
因此,我们的主干思想是:利用单位复根的性质,巧妙的求值/插值,使得我们在$O(nlogn)$的时间内完成这些操作。
简图(远航之曲大佬的图):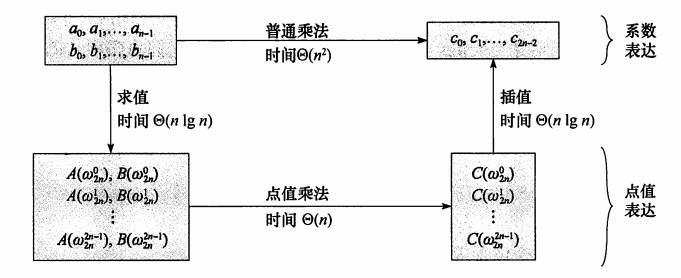
DFT
就是快速带入点值的过程。
我们的多项式:$A(x)=a_0x^0+a_1x^1+a_2x^2…+a_{n-1}x^{n-1}$。其中$a_0,a_1…a_n$是系数(题目给定)。
接下来,我们设$n=2^k$。不足的地方用$0$补齐。
把它的系数按下表奇偶分组(指数还是顺序下来的):
$A_0(x)=a_0x^0+a_2x^1+a_4x^2…+a_{n-2}x^{n/2-1}$
$A_1(x)=a_1x^0+a_3x^1+a_5x^2…+a_{n-1}x^{n/2-1}$
易得$A(x)=A_0(x^2)+xA_1(x^2)$。
那么,我们代入$x=w_n^0,w_n,w_n^2…w_{n}^{n-1}$。
考虑求前面$n/2$个,然后直接得到后面$n/2$个。令$k\in [0,n/2)$,则:
$A(w_n^k)=A_0(w_n^{2k})+w_n^kA_1(w_n^{2k})$
然后我们再代入$w_n^{k+n/2}=-w_n^k$:
$A(w_n^{k+n/2})=A_0(w_n^2k)-A_1(w_n^2k)$
我们发现,$w_n^{k+n/2}=-w_n^k$。然而$A_0,A_1$里面是$x^2$,所以取负不影响$A_0$和$A_1$的结果,只有$A_1$前面那一项有一个正负号的区别!
所以,我们求出前一半,就珂以$O(n)$求出后一半。
这样显然是$O(nlogn)$的。
DFT的实现优化
刚刚做完$O(nlogn)$的式子。但是,实现的时候,递归似乎太慢了,还不如暴力来的快。
我们观察一下,被奇偶分组后的下标。
(草 图)
转换一下二进制:
000 001 010 011 100 101 110 111
变成:
000 100 010 110 001 101 011 111
相当于每个二进制数位反过来了。
然后我们通过递推,推出最后的状态。然后不断合并,合并成答案。成功的把递归转化掉了。这样还是$O(nlogn)$,但是快了很多!
IDFT
IDFT,就是我们已知一个点值表示的多项式,而且代入的点值还是$w_n^0,w_n^1…w_n^{n-1}$。
我们设出系数$a_0,a_1..a_{n-1}$,列出方程:
用矩阵表达:
设这个式子是“珂朵莉IDFT①式”
然后设矩阵$D$,$D$中的每一项和左边那个矩阵
中对应位置上的项,都是倒数。
已证,$D\times V=n\times I_n$,其中$I_n$是$n$阶单位矩阵。
那也就是,$D=\dfrac{1}{n}V^{-1}$
把“珂朵莉IDFT①式”中,左右两边同时乘一个$D=\dfrac{1}{n}V^{-1}$。
易得:
那么我们把矩阵$V$中,所有项取倒数,然后做一遍$DFT$即珂。最后记得除一个$n$。
模板题的代码
洛谷 38031
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
using namespace std;
namespace Flandre_Scarlet
{
//2097153=2^21+1
void R1(int &x)
{
x=0;char c=getchar();int f=1;
while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=(f==1)?x:-x;
}
void Rd(int cnt,...)
{
va_list args;
va_start(args,cnt);
F(i,1,cnt)
{
int* x=va_arg(args,int*);R1(*x);
}
va_end(args);
}
struct cp{real R,I;}; //复数类
//R: 实部,a+bi中的a
//I:虚部,a+bi中的b
cp operator+(cp a,cp b){return (cp){a.R+b.R,a.I+b.I};}
cp operator-(cp a,cp b){return (cp){a.R-b.R,a.I-b.I};}
cp operator*(cp a,cp b){return (cp){a.R*b.R-a.I*b.I,a.R*b.I+a.I*b.R};}
int n,m;
cp a[N],b[N];
void Input()
{
Rd(2,&n,&m);
F(i,0,n) {int x;R1(x);a[i].R=x;}
F(i,0,m) {int x;R1(x);b[i].R=x;}
}
int r[N],lim;
void FFT(cp A[],int type)
//type=1: DFT
//type=-1: IDFT
{
F(i,0,lim) if (i<r[i]) swap(A[i],A[r[i]]);
for(int mid=1;mid<lim;mid<<=1) //合并区间的长度
//每次合并两个长度为mid的区间
{
cp Wn=(cp){cos(Pi/mid),type*sin(Pi/mid)};
//把虚部乘以-1,相当于变成一个实数,其值为向量长度
//由于向量在单位圆上,长度为1,就相当于取倒数了
for(int j=0;j<lim;j+=(mid<<1))
{
cp w=(cp){1,0}; //Wn^0
for(int k=0;k<mid;++k,w=w*Wn) //w:不断代入Wn^k
{
cp X=A[j+k],Y=w*A[j+mid+k];
//DFT的合并式子
A[j+k]=X+Y;
A[j+mid+k]=X-Y;
}
}
}
}
void Soviet()
{
int l=0;lim=1;
while(lim<=n+m) lim<<=1,++l;
F(i,0,lim) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
FFT(a,1);FFT(b,1); //两个DFT
F(i,0,lim) a[i]=a[i]*b[i]; //点值乘法
FFT(a,-1); //IDFT
F(i,0,n+m) printf("%d ",(int)(a[i].R/lim+0.5)); //还要乘一个1/lim
//+0.5是取四舍五入
putchar('\n');
}
Flan IsMyWife()
{
Input();
Soviet();
}
}
int main(){
Flandre_Scarlet::IsMyWife();
getchar();getchar();
return 0;
}
NTT
NTT本质上就是把$FFT$中的单位复根换成一个有相同性质的整数:原根。
只要记住$998244353$的原根是$3$即珂。
然后和$FFT$同样的方法去写就珂以了,也是DFT+IDFT。
就是把里面单位复根换成原根,一样写即可。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
namespace Flandre_Scarlet
{
void R1(int &x)
{
x=0;char c=getchar();int f=1;
while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=(f==1)?x:-x;
}
void Rd(int cnt,...)
{
va_list args;
va_start(args,cnt);
F(i,1,cnt)
{
int* x=va_arg(args,int*);R1(*x);
}
va_end(args);
}
int n,m;
int a[N],b[N];
void Input()
{
Rd(2,&n,&m);
F(i,0,n) R1(a[i]);
F(i,0,m) R1(b[i]);
}
int qpow_p(int a,int b,int m) //正数的快速幂
{
int r=1;
while(b)
{
if (b&1) r=r*a%m;
a=a*a%m,b>>=1;
}
return r;
}
int qpow(int a,int b,int m) //支持负指数的快速幂(就是先求快速幂,然后求一个逆元)
{
if (b==0) return 1;
else if (b<0) return qpow_p(qpow_p(a,-b,m),m-2,m);
else return qpow_p(a,b,m);
}
int r[N],lim;
void NTT(int A[N],int type)
{
F(i,0,lim) if (i<r[i]) swap(A[i],A[r[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
int Wn=qpow(qpow(3,type,mod),(mod-1)/(mid<<1),mod);
for(int j=0;j<lim;j+=(mid<<1))
{
int w=1;
for(int k=0;k<mid;k++,w=(w*Wn)%mod)
{
int X=A[j+k],Y=w*A[j+mid+k]%mod;
A[j+k]=(X+Y)%mod;
A[j+mid+k]=(X-Y+mod)%mod;
}
}
}
}
void Soviet()
{
lim=1ll;int l=0;
while(lim<=n+m) lim<<=1ll,++l;
F(i,0,lim) r[i]=(r[i>>1ll]>>1ll)|((i&1ll)<<(l-1));
NTT(a,1);NTT(b,1);
F(i,0,lim) a[i]=(a[i]*b[i])%mod;
NTT(a,-1);
int iv=qpow(lim,-1,mod);
F(i,0,n+m) printf("%lld ",a[i]*iv%mod); //*iv相当于除以一个lim
putchar('\n');
}
Flan IsMyWife()
{
Input();
Soviet();
}
}
int main(){
Flandre_Scarlet::IsMyWife();
getchar();getchar();
return 0;
}
NTT的好处和坏处
好处: 和FFT相比,把浮点数换成整数。常数很小,而且避免了精度问题
坏处: 小心溢出!(超过NTT模数也是一种溢出,会导致答案不同)(如果让你对某个数取模那另说)