今天日常给同学@CollinGao 写奥♂义。讲到了这个东西,还是挺有用的,就是有点毒瘤?仿佛没什么人知道的亚子。。。
不是很难理解的算法,我在期中考试考场上就直接yy出了一个来。虽然马上CSP了,但是我还是准备来颓废,写写这篇奥♂义。
基础题型
给你一个字符串,对于每个前缀,求该前缀中有多少前缀不同的回文子串。定义一个回文子串的权值为:长度乘以出现次数。对于每个前缀,也请你求出最大的回文子串的权值是多少。
回文自动机(又名回文树)是干啥的
大家都知道TRIE树(知道即珂,但是如果连听说都没听说过,那劝退了)。在TRIE树上,每个节点表示一个字符串,字符记录在边权上。连一条边表示在这个字符串后面加上一个字符。
那么,回文自动机是怎么弄的的?连一条边,表示在这个字符串前后各加上一个字符。比如某个父亲的字符串为”aba”,连了一条权值为’c’的边到儿子,儿子的字符串就是”cabac”。
然后要注意一点,回文自动机有两个根。其原因很显然,因为一个父亲以下的字符串长度的奇偶性不会改变。所以,两个根分别记录奇数长度和偶数长度的回文串,名字就叫奇根和偶根。偶根很好理解,表示一个空串,其长度为$0$。那么,奇根怎么办呢?仔细一推,单个字符长度为$1$,其父亲的长度为其长度$-2$,也就是说,奇根表示的字符串长度为$-1$?!
没事,$-1$就$-1$,只不过是为了方便计算罢了。实际实现中,考虑到空间问题,我们并不会实际记录表示的字符串,只是记录一个长度$len$。那么,只要让这个点的$len=-1$即珂,一点问题都没有。
fail指针
精髓(准确来讲,是每个自动机的精髓)。对于一个节点,它的$fail$指针是指:除了自己之外,LPS(Longest Palindrome Suffix,最长回文后缀)所对应的点。
如果你仔细咀嚼了这句话,那么你会想这样一个问题:除了自己之外的最长回文子串一定在树上能找到吗?
证明fail一定在树上能找到
(如果您能自己证明,请跳过这段)
设当前节点表示字符串$s$,$fail$指向的节点所对应为$f$,$f^t$表示把$f$反过来,$|f|$表示$f$的长度,如图所示。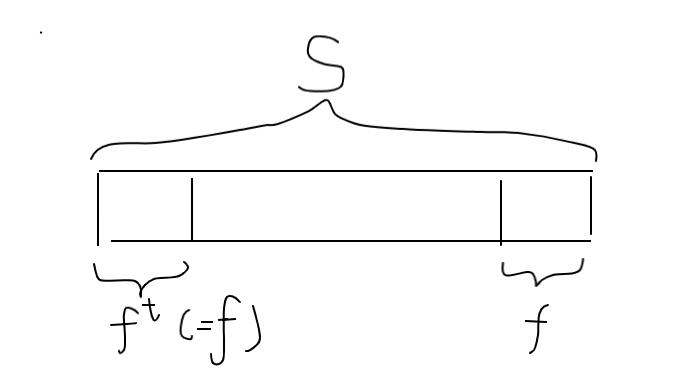
由于$S$是回文串(根据定义),$S$的前缀$|f|$个字符串和后缀$|f|$。$S$和$f$都是回文的,非常容易证明,$S$的$|f|$个前缀和这么长的后缀是一样的。
那么,$f$在后面出现一遍,就说明在前面也出现了一遍。由于我们是从前往后加入到树上的,所以这个串一定能找到。
证毕 $\blacksquare$
如何构建
上面讲了一下,我们是按照从前往后的顺序插入$s$的每个字符的。对于插入第$i$个位置,我们的任务是找到其$LPS$,并把它插入到树上的正确位置。那么,如何找到呢?
等价一下,这个节点满足:
- 它是i-1位置的一个回文后缀
- 它左右字符相等,都是$s[i]$
对于满足条件1,我们记录一个$last$,表示$i-1$插入在了树上哪个位置。(当我们插入完$i$的位置的时候,我们令它为我们找到的位置,即珂维护)
然后$last$显然就是$i-1$的一个回文后缀。但是我们要找到所有的回文后缀,那没问题,我们不断的跳$fail$即珂。
然后还要满足条件2。设现在我们跳到了点$cur$,这个点上的长度值为$len(cur)$。只要判断$s[i]==s[i-len(cur)-1]$即珂。如果满足就退出,不满足就$cur=fail(cur)$,继续循环。
关于$fail$的维护:很简单,和上面找到父亲的过程只差一个$cur$初始值的区别。因为$fail$指针要满足不等于自己,所以,$cur$的初始值,不是$father$,而是$fail(father)$。和找到父亲的步骤还有一点点不同,就是最后找到一个$cur$满足$s[i]==s[i-len(cur)-1]$的时候,返回的不是$cur$而是$cur$的边权为$s[i]$的儿子。这里还有一个至关重要的细节要注意,先求出fail指针,才能连边。代码中会提到。
那么我们来举一个例子。我们要构建的字符串s=”bilibili”。
初始化,构建奇根和偶根。红色是奇根,绿色是偶根。特殊地(忘了讲了),奇根和偶根的$fail$指针(黄色)互相指向对方。
第一步,插入位置$1$。默认是插入到$0$上,失败了再跳$fail$。我们发现,$s[1]!=s[1-len(0)-1]$,于是跳了$fail(0)=1$,然后显然满足了。我们还发现,此时还没有节点,便新建一个节点(编号为$2$),把它接在奇根($1$)下面。跳一下$fail$,发现$fail$是$0$(显然)。由于很多节点的$fail$都是$0$,这些边我就不连了(为了看起来美观)。效果图: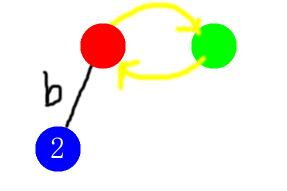
时间关系,我们不仔细看每一个位置的插入过程,直接跳到第$5$个位置的插入。这之前的图建出来长这样: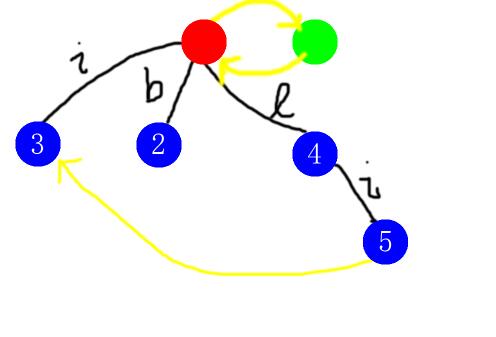
然后我们大喊一声:King Crimson!
第五步,插入位置$5$,此时前缀为$bilib$。默认插入在$last$上,也就是编号$5$的位置。我们一下就满足了条件,所以我们的确要接在$last$下面。求一下$fail$指针,先到$fail(5)=3$试一下,发现,不行。然后跳到$fail(3)=0$试一下,还不行,跳到$fail(0)=1$再试一下,行了,返回$1$的边权为$si$的儿子,也就是编号为$2$的节点。完成之后,图长这样: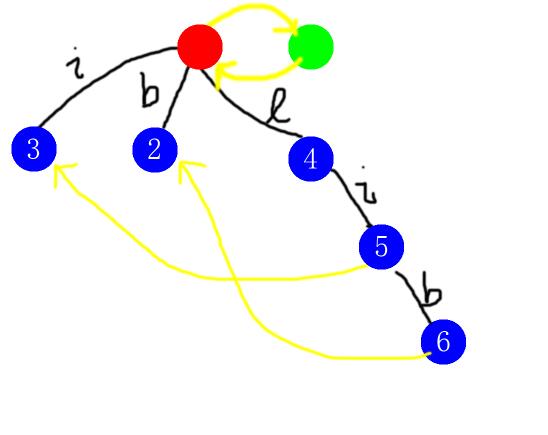
让我们再大喊一声:King Crimson!
最终完成图: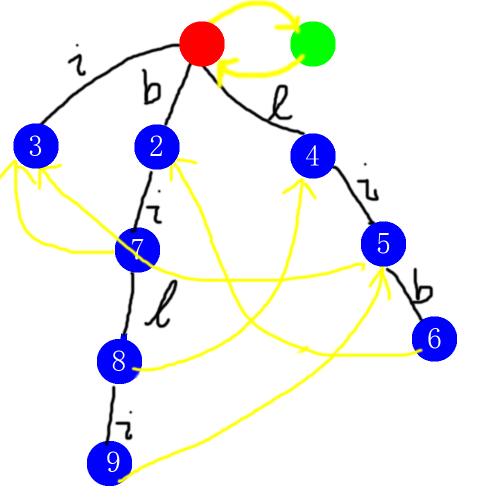
然后我们这就构建好了一个回文自动机。
附:
“我的讲义,能抄下来么?”
“能抄一点。”
“让我康康!”
“你看,这个fail边,应该连在儿子这里的。尽管你这样画很好看,但这个fail边就是这样连的,你不能改变它”
我心里还是有点不服气。图还是我画的好,至于这条边到底连在哪里,我自然是知道的。
—— 选自 鲁迅《藤野先生》
实现(你们最想要的
1 | class Palindrome_Tree //我喜欢写面向对象 |
应用
我们讲了这么多,来解决些实际问题。
本质不同的回文串个数
每个点(除了奇根和偶根)都一一对应一个本质不同的回文串。只要输出$cnt-1$即珂。(应该是点数-2,但是由于我是从0开始算点的,所以-1才是正确的)每个回文串的个数
每个点维护一个值$cnt$(重名了,但是因为命名空间不一样,写在struct里,所以不会报错)。然后插入一个点时,找到它所在的树上位置,该点上$cnt++$。最后再$cnt[fail(i)]+=cnt[i]$,i从$n$到$1$。和$KMP$中计算每个前缀出现的次数是类似的原理。
尝试一下: