洛谷 5947 [POI2003]Trinomial 题解

题意简述

$T$组数据。给定$n,m$，求$(x^2+x+1)^n$中，$x^m$项的系数是多少。答案对$3$取膜。
（这个膜数很神奇！注意！突破点就在这！）

$T<=1e4$，$n<=1e15$，$m<=2n$。

思路框架

答案是$C_{2n}^m\times (m\% 2+1)$，对$3$取膜（写个$Lucas$即可）

具体思路

首先，我们分括号讨论。因为是$(x^2+x+1)^n$，所以有$n$个括号，并且每个括号可以出$x^2,x,1$。然后我们要求，有多少种方案使得每个括号中出的数积为$x^m$。

我们开始打草稿：我们把$n$个括号从$1$到$n$顺序编号，每个括号上面有两个复选框。打了几个勾，就是代表出$x$的多少次方。具体来说就是：
一个都没打勾，代表出$x^0$（$x^0$就是$1$）；其中一个打了勾，代表出$x$；两个都打了勾，代表出$x^2$。

如图所示是$n=4$的情况：

我们这样勾选：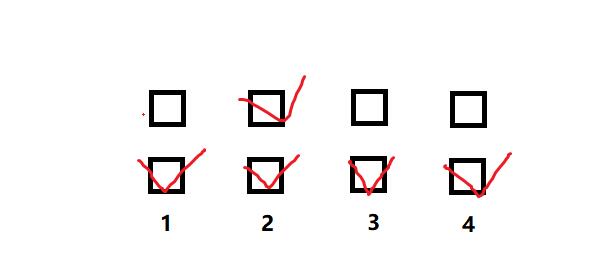

那就相当于：
第一个括号出$x$
第二个括号出$x^2$
第三个括号出$x$
第四个括号出$x$
那它就会给$x^5$那一项贡献一种情况。

那么我们现在考虑$x^m$项的系数，换句话说就是有多少种方法凑出$x^m$。

显然，上面的复选框中，我们每打一个勾，乘出来就多一个$x$。（上面打了$5$个勾，乘起来就是$x^5$）然后一共有$2n$个复选框，所以答案就是$C_{2n}^m$。

这就完了？不！这样考虑有重复的！

假如第$i$个括号出的是$x$，那就相当于在$i$上面两个复选框中，其中一个要打勾。而我们只在意数量，具体打勾打上面那个框还是下面的那个，是一样的。那就会把一个答案算两遍，所以要除以$2$。

假设我们有$k$个括号出的是$x$，那么我们的答案就要除以一个$2^k$。

首先，$k$和$m$肯定是同奇偶的。

稍微证一下（会证跳过）： 有$k$个括号出$x$，那剩下$x^{m-k}$都是由出$1$或$x^2$组成的。$m-k$由若干个$0$和$2$相加而成，所以$m-k$是偶数。所以$m$和$k$同奇偶。

然后，在模三意义下，2的逆元就是其本身！所以，除以一个$2^k$，就相当于乘以一个$2^k$。

还没完，我们继续化。我们发现，$2$的幂除以$3$的余数是：$2,1,2,1,2,1…$。具体点说，$2^k\% 3=(k\% 2)+1$。而$k$和$m$又同奇偶，所以，所有的$k\% 2+1$都等于$m\% 2+1$。

综上，我们的答案就是$C_{2n}^m\times (m\% 2+1)$。

代码

复制

#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
    #define int long long 
    #define F(i,l,r) for(int i=l;i<=r;++i)
    #define D(i,r,l) for(int i=r;i>=l;--i)
    #define Fs(i,l,r,c) for(int i=l;i<=r;c)
    #define Ds(i,r,l,c) for(int i=r;i>=l;c)
    #define MEM(x,a) memset(x,a,sizeof(x))
    #define FK(x) MEM(x,0)
    #define Tra(i,u) for(int i=G.Start(u),__v=G.To(i);~i;i=G.Next(i),__v=G.To(i))
    #define p_b push_back
    #define sz(a) ((int)a.size())
    #define iter(a,p) (a.begin()+p)
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Rd(int cnt,...)
    {
        va_list args;
        va_start(args,cnt);
        F(i,1,cnt) 
        {
            int* x=va_arg(args,int*);R1(*x);
        }
        va_end(args);
    }

    int n,m;
    void Input()
    {
        Rd(2,&n,&m);
    }

    int c[4][4];
    int C(int n,int m) //卢卡斯定理求C(n,m)%3
    {
        if (n==0 and m==0) return 1;
        return C(n/3,m/3)*c[n%3][m%3]%3;
    }
    void Soviet()
    {
        c[0][0]=1;
        c[1][1]=c[1][0]=1;
        c[2][0]=c[2][2]=1;c[2][1]=2; //预处理<3的组合数
        printf("%lld\n",C(2*n,m)*(m%2+1)%3); //用上面的式子
    }

    #define Flan void
    Flan IsMyWife()
    {
        int t;R1(t);
        F(i,1,t)
        {
            Input();
            Soviet();
        }
    }
    #undef int //long long 
}
int main(){
    Flandre_Scarlet::IsMyWife();
    getchar();getchar();
    return 0;
}