题意简述
老铁们,虽然不是同一个题目,但是是一样的题意,今天我来给大家打一个暴力模拟线段树,奥利给
一个长度为 $n$ 的序列,初始全 $0$ 。有 $m$ 次修改操作。给你两个常数 $p,q$,第 $i$ 次操作会把第 $(i\times p+q)\mod n+1$ 和 $(i\times q+p)\mod n+1$ 之间的所有数赋值为 $i$。求出最后$n$个数的状态。
$n\le 10^6,m\le 10^7$。
思路框架
这个是不一样的做法,是线段树+一点点思维优化。
(大家似乎都是写的链表做法啊…我不会打链表啊…)
我们发现$(i\times p+q)\mod n+1$这个式子,可以先把$i$对$n$取膜之后再算!!!也就是说,有很多次区间覆盖操作都是覆盖的同一块区间!
那么本质不同的修改操作就只有$n$个,再加上最后$m\mod n$个除不尽的。
特判$m<n$的情况。
无论哪种情况,复杂度都是$O(n \log n)$的。对于$n\le 10^6$的数据,足够了。
具体思路
显然,在同一个同余系里,最后面那次覆盖的颜色是答案。那么我们把$m$次操作,每$n$个分一块(除不尽的先不管)。显然,最后一块的操作可以把前面几块的操作全部都覆盖掉。所以最后一块是唯一有用的一块。
$m$除以$n$,可以画出这样的图:
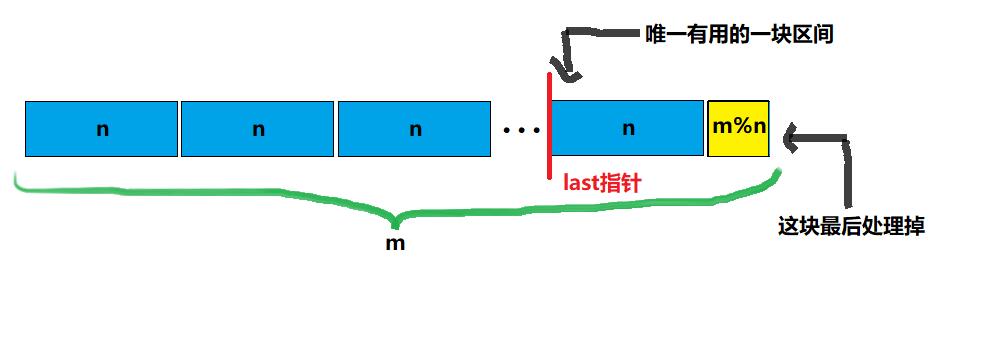
last指针表示最后一块有用的区间前面一个位置,那么最后一块有用的染色操作就是$i=last+1,last+2\cdots last+n$的时候。
容易计算出 last 指针为:$n(\lfloor\dfrac{m}{n}\rfloor-1)$
最后$m\mod n$个特判掉。
代码
1 |
|