Codeforces 1304E 1-Trees and Queries 题解

发表于 | 阅读次数：
本文字数： 1.1k 字 | 阅读时长 ≈ 5 分钟

题意简述

$n$ 个节点的树，每条边权都是 $1$。有 $q$ 个询问，每次给定 $x,y,a,b,k$，表示你在树上加一条边 $(x\leftrightarrow y)$ ，并求从 $a$ 到 $b$ 走 $k$ 条边的最短路。其中每条边和点都允许重复经过。求完询问后，把 $(x\leftarrow y)$ 这条边删掉（即：询问之间都是独立的）。

$n\le 1e5; q\le 1e5; 1\le x,y,a,b \le n; 1\le k \le 1e9$

思路框架

首先倍增LCA维护两点之间的最短路。

由于边能重复经过，参考今年普及 T4 的思路，我们只要找一条长度 $\le k$ 并且和 $k$ 同奇偶的路即可。

原先$a,b$之间的最短路只能有一条。但是加上边 $x,y$ 之后，就多了两条：
$a\rightarrow x \rightarrow y \rightarrow b$，长度为 $Q(a,x)+1+Q(y,b)$
$a\rightarrow y \rightarrow x \rightarrow b$，长度为 $Q(a,y)+1+Q(x,b)$
（其中 $Q(u,v)$ 表示 $u$ 到 $v$ 的最短路，代码里叫PathLen）
这三条里面判断一下，哪条能满足：长度 $\le k$ 且长度和$k$同奇偶

有一个就输出YES，否则NO。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
    #define N 155555
    #define F(i,l,r) for(int i=l;i<=r;++i)
    #define D(i,r,l) for(int i=r;i>=l;--i)
    #define Fs(i,l,r,c) for(int i=l;i<=r;c)
    #define Ds(i,r,l,c) for(int i=r;i>=l;c)
    #define MEM(x,a) memset(x,a,sizeof(x))
    #define FK(x) MEM(x,0)
    #define Tra(i,u) for(int i=G.Start(u),__v=G.To(i);~i;i=G.Next(i),__v=G.To(i))
    #define p_b push_back
    #define sz(a) ((int)a.size())
    #define iter(a,p) (a.begin()+p)
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Rd(int cnt,...)
    {
        va_list args;
        va_start(args,cnt);
        F(i,1,cnt) 
        {
            int* x=va_arg(args,int*);R1(*x);
        }
        va_end(args);
    }
    class Graph
    {
        public:
            int head[N];
            int EdgeCount;
            struct Edge
            {
                int To,Label,Next;
            }Ed[N<<1];
            void clear(int _V=N,int _E=N<<1) 
            {
                memset(Ed,-1,sizeof(Edge)*(_E));
                memset(head,-1,sizeof(int)*(_V));
                EdgeCount=-1;
            }
            void AddEdge(int u,int v,int w=1)
            {
                Ed[++EdgeCount]=(Edge){v,w,head[u]};
                head[u]=EdgeCount;
            }
            void Add2(int u,int v,int w=1) {AddEdge(u,v,w);AddEdge(v,u,w);}
            int Start(int u) {return head[u];}
            int To(int u){return Ed[u].To;}
            int Label(int u){return Ed[u].Label;}
            int Next(int u){return Ed[u].Next;}
    }G;
    int n;
    void Input()
    {
        R1(n);
        G.clear();
        F(i,1,n-1)
        {
            int u,v;Rd(2,&u,&v);
            G.Add2(u,v);
        }
    }

    int fa[N][22],deep[N];
    void DFS(int u,int f)
    {
        deep[u]=(u==f)?0:deep[f]+1; //deep[i] 表示从 i 到根经过的 **边数** 
        //所以 deep[根] 是 0 哦
        fa[u][0]=f; 
        F(i,1,20) fa[u][i]=fa[fa[u][i-1]][i-1];
        Tra(i,u)
        {int v=__v;
            if (v!=f) DFS(v,u);
        }
    }
    int LCA(int a,int b) //求a,b的LCA
    {
        if (deep[a]<deep[b]) swap(a,b);
        D(i,20,0) if (deep[fa[a][i]]>=deep[b]) a=fa[a][i];
        if (a==b) return a;
        D(i,20,0) if (fa[a][i]!=fa[b][i]) a=fa[a][i],b=fa[b][i];
        return fa[a][0];
    }
    int PathLen(int a,int b) 
    {
        return deep[a]+deep[b]-2*deep[LCA(a,b)];
    }
    bool cxk(int path,int k){return path<=k and (k-path)%2==0;}
    void Soviet()
    { 
        DFS(1,1);
        int q;R1(q);
        F(i,1,q)
        {
            int a,b,x,y,k;
            Rd(5,&x,&y,&a,&b,&k);
            int path1=PathLen(a,b);
            int path2=PathLen(a,x)+1+PathLen(y,b);
            int path3=PathLen(a,y)+1+PathLen(x,b); //上面讨论的三条路
            if (cxk(path1,k) or cxk(path2,k) or cxk(path3,k)) puts("YES");
            else puts("NO");
        }
    }

    #define Flan void
    Flan IsMyWife()
    {
        Input();
        Soviet();
    }
}
int main()
{
    Flandre_Scarlet::IsMyWife();
    getchar();getchar();
    return 0;
}

后记： 版权问题

（不想看就算了）
考场上，我想出了这个算法（第一个）。然后我把这个算法告诉了我的好朋友lym。他又把这个算法告诉了他的好朋友zhk。

最近zhk也像我一样搭了一个hexo博客，他就来找我帮他调试博客的功能。然后我发现了他有一篇文章，就是这个的题解，同步发表于洛谷博客的。我一看这思路似乎很眼熟，便去问他你是怎么想出这思路的。

（开始回溯）他说，是lym告诉他的，lym给了他一张截图。

截图：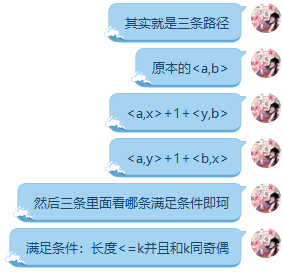

你们看这个头像和我的是否有几分相像呢（滑稽）。这真是 缘 分 的 天 空 啊。

w