codeforces 916E Jamie and Tree 题解

发表于 | 阅读次数：
本文字数： 1.9k 字 | 阅读时长 ≈ 10 分钟

题意简述

给定一个 $n\le 10^5$ 个点带权的树，初始根为 $1$。支持三种操作：
1 r 把根换成 $r$
2 u v x 把 $LCA(u,v)$ 的子树整体加 $x$
3 u 查询 $u$ 的子树点权和

操作数$\le 10^5$。每个点权 $\le 10^8$ 。

思路

如果没有 $1$ 操作，那 $2,3$ 操作显然就是一个板子。

但是现在有了 $1$ 操作。 那么我们就要考虑几个问题：

  1. 如何求 LCA
  2. 如何知道子树是哪一块 （对其进行求和或加值）

当然，无根树肯定是不好讨论的。我们先假定 $1$ 为根。 然后判断以 $r$ 为根的子树长什么样。

为了不混淆，设：
$LCA(u,v,r)$ 表示以 $r$ 为根，$u,v$ 的 $LCA$。
$SUB(u,r)$ 表示以 $r$ 为根，$u$ 的子树。

路径不需要重新定义，因为路径是唯一确定的，和根无关。

求LCA

假设我们要求 $LCA(u,v,r)$。

  1. 如果当前的根 $r$ 在 $u,v$ 的路径上，那么显然 $LCA(u,v,r)=r$。
  2. 否则，设 $L=LCA(u,v,1)$。 如果当前的根在 $SUB(L,1)$ 外，那么 $LCA(u,v,r)=L$，就不会有影响
  3. 再否则，$LCA(u,v,r)$ 就是 $u,v$ 路径上的某个点了。稍微想一下，这个点是 $LCA(u,r,1)$ 或者 $LCA(v,r,1)$ 中的一个。 再仔细想想，似乎是选深的那一个（以 $1$ 为根）。那么如果同样深怎么办呢？
    继续想想，$LCA(u,r,1)$ 和 $LCA(v,r,1)$ 肯定一个是 $LCA(u,v,1)$ ，一个是 $LCA(u,v,r)$。如果深度相同，那就说明 $LCA(u,r,1)=LCA(v,r,1)=LCA(u,v,1)$ 。这个时候选哪个也无所谓了，反正都是对的。

求某个子树

假设我们要求 $SUB(u,r)$

  1. $u=r$。 最简单的情况，子树就是整棵树 （但是不能忘记特判！）
  2. $r$ 在 $SUB(u,1)$ 之外。 这也很显然，$SUB(u,r)=SUB(u,1)$。
  3. 关键问题就是 $r$ 在 $SUB(u,1)$ 之内的情况咋整。

我们画一张图：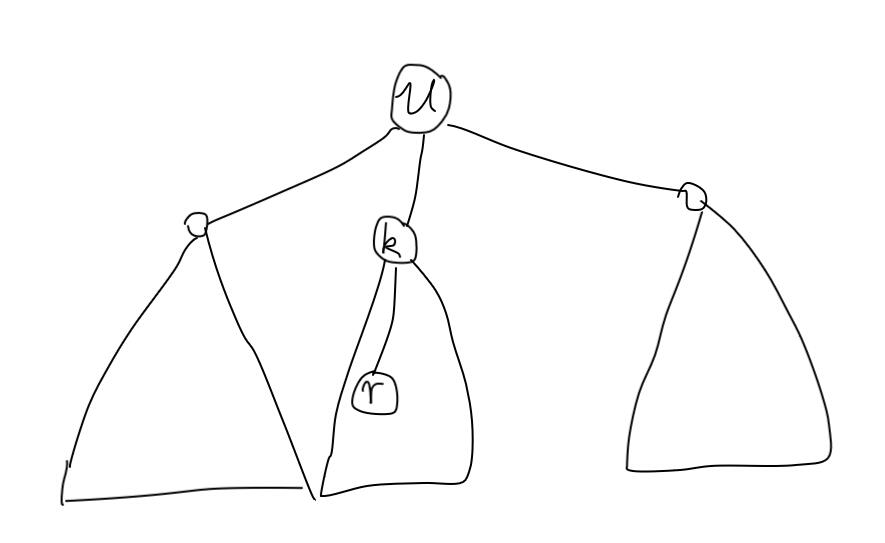

很明显，此时 $SUB(u,r)$ 就等于整棵树中减去 $SUB(k,1)。（这张图有一个没画全的地方，就是 $u$ 上面可能还有别的点）

而 $k$ 的值，也就是 $r$ 在 $u$ 的哪个子树里面，这个可以用倍增求。

总结

我们发现，最后的操作，只有子树加减，和单点求和的操作。甚至不用写树链剖分。这个用 $DFS$ 序维护就能解决。

代码

点击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
    #define N 255555
    #define int long long 
    #define F(i,l,r) for(int i=l;i<=r;++i)
    #define D(i,r,l) for(int i=r;i>=l;--i)
    #define Fs(i,l,r,c) for(int i=l;i<=r;c)
    #define Ds(i,r,l,c) for(int i=r;i>=l;c)
    #define MEM(x,a) memset(x,a,sizeof(x))
    #define FK(x) MEM(x,0)
    #define Tra(i,u) for(int i=G.Start(u),v=G.To(i);~i;i=G.Next(i),v=G.To(i))
    #define p_b push_back
    #define sz(a) ((int)a.size())
    #define iter(a,p) (a.begin()+p)
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Rd(int cnt,...)
    {
        va_list args;
        va_start(args,cnt);
        F(i,1,cnt) 
        {
            int* x=va_arg(args,int*);R1(*x);
        }
        va_end(args);
    }
    class Graph
    {
        public:
            int head[N];
            int EdgeCount;
            struct Edge
            {
                int To,Label,Next;
            }Ed[N<<1];
            void clear(int _V=N,int _E=N<<1) 
            {
                memset(Ed,-1,sizeof(Edge)*(_E));
                memset(head,-1,sizeof(int)*(_V));
                EdgeCount=-1;
            }
            void AddEdge(int u,int v,int w=1)
            {
                Ed[++EdgeCount]=(Edge){v,w,head[u]};
                head[u]=EdgeCount;
            }
            void Add2(int u,int v,int w=1) {AddEdge(u,v,w);AddEdge(v,u,w);}
            int Start(int u) {return head[u];}
            int To(int u){return Ed[u].To;}
            int Label(int u){return Ed[u].Label;}
            int Next(int u){return Ed[u].Next;}
    }G;
    class SegmentTree //线段树 区间加 区间求和
    {
    public:
        struct node{int l,r,s,a;}tree[N<<2];
        #define ls index<<1
        #define rs index<<1|1

        #define L tree[index].l
        #define R tree[index].r
        #define S tree[index].s
        #define A tree[index].a
        #define lL tree[ls].l
        #define lR tree[ls].r
        #define lS tree[ls].s
        #define lA tree[ls].a
        #define rL tree[rs].l
        #define rR tree[rs].r
        #define rS tree[rs].s
        #define rA tree[rs].a
        void Update(int index=1)
        {
            S=lS+rS;
        }
        void Build(int l,int r,int index=1)
        {
            L=l,R=r;S=A=0;
            if (l==r) {return;}
            int mid=(l+r)>>1;
            Build(l,mid,ls); Build(mid+1,r,rs);
            Update(index);
        }
        void AddOne(int x,int index=1)
        {
            A+=x;
            S+=(R-L+1)*x;
        }
        void PushDown(int index=1)
        {
            if (A) {AddOne(A,ls); AddOne(A,rs); A=0;}
        }
        void Add(int l,int r,int x,int index=1)
        {
            if (l>R or L>r) return;
            if (l<=L and R<=r) return AddOne(x,index);
            PushDown(index);
            Add(l,r,x,ls); Add(l,r,x,rs);
            Update(index);
        }
        int  Query(int l,int r,int index=1)
        {
            if (l>R or L>r) return 0;
            if (l<=L and R<=r) return S;
            PushDown(index);
            return Query(l,r,ls)+Query(l,r,rs);
        }
    }T;
    
    int n,m;
    int a[N];
    void Input()
    {
        Rd(2,&n,&m);
        F(i,1,n) R1(a[i]);
        G.clear();
        F(i,1,n-1) {int u,v;Rd(2,&u,&v); G.Add2(u,v);}
    }

    int In[N],Out[N],Time=0; 
    int fa[N][22],deep[N];
    void DFS(int u,int f)
    {
        In[u]=++Time;
        deep[u]=(u==f)?0:deep[f]+1;
        fa[u][0]=f; F(i,1,20) fa[u][i]=fa[fa[u][i-1]][i-1];
        Tra(i,u) if (v!=f)
        {
            DFS(v,u);
        }
        Out[u]=Time;
    }
    int FindSon(int u,int f) //求 u 在 f 的哪个子树里 （u相对于f的k值）
    {
        D(i,20,0) if (deep[fa[u][i]]>deep[f]) u=fa[u][i];
        return u;
    }
    bool IsFa(int u,int f) //这个判断f是否是u的祖先
    {
        if (deep[u]<deep[f]) return false;
        if (u==f) return true;
        return fa[FindSon(u,f)][0]==f;
    }
    //upd: 傻了，这个直接DFS序判断即可
    int LCA(int u,int v)
    {
        if (deep[u]<deep[v]) swap(u,v);
        D(i,20,0) if (deep[fa[u][i]]>=deep[v]) u=fa[u][i];
        if (u==v) return u;
        D(i,20,0) if (fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
        return fa[u][0];
    }
    //非常正常的LCA
    bool OnPath(int u,int v,int k)
    {
        int l=LCA(u,v);
        if (l==k) return true;
        return !IsFa(l,k) and (IsFa(u,k) or IsFa(v,k));
    }
    //判断k是否在u,v路径上
    void SubtAdd(int u,int x){T.Add(In[u],Out[u],x);}
    //子树加
    int  SubtSum(int u) {return T.Query(In[u],Out[u]);}
    //子树求和
    void Soviet()
    {
        DFS(1,1);
        T.Build(1,n);
        F(i,1,n) T.Add(In[i],In[i],a[i]); //初始化
        int root=1; //这个别忘了
        F(i,1,m)
        {
            int o;R1(o);
            if (o==1)
            {
                int u;R1(u);
                root=u; //非常简单的换根操作
            }
            if (o==2)
            {
                int u,v,x;Rd(3,&u,&v,&x);
                int l=LCA(u,v);
                if (OnPath(u,v,root)) 
                {
                    //特判: 如果root在u,v路径上，那么LCA(u,v,root)==root，直接加整个树
                    T.Add(1,n,x);
                }
                else if (In[root]<In[l] or Out[l]<In[root]) 
                {
                    //如果root不在x子树内，那么没有影响，和根为1情况一样
                    SubtAdd(l,x);
                }
                else
                {
                    T.Add(1,n,x); //整个加
                    if (deep[LCA(root,u)]<deep[LCA(root,v)]) swap(u,v);
                    int k=FindSon(root,LCA(root,u));
                    //找到k
                    SubtAdd(k,-x);
                    //把k的子树减掉
                }
            }
            if (o==3)
            {
                int u;R1(u);
                //这个和上面类似的
                if (root==u) 
                {
                    printf("%lld\n",T.Query(1,n));
                }
                else if (In[root]<In[u] or Out[u]<In[root]) 
                {
                    printf("%lld\n",SubtSum(u));
                }
                else 
                {
                    int k=FindSon(root,u);
                    printf("%lld\n",T.Query(1,n)-SubtSum(k));
                    //整棵树-k的子树
                }
            }
        }
    }

    #define Flan void
    Flan IsMyWife()
    {
        Input();
        Soviet();
    }
    #undef int //long long 
}
int main()
{
    Flandre_Scarlet::IsMyWife();
    getchar();getchar();
    return 0;
}
w