算法讲解
(本篇文章假设您学过莫比乌斯反演 (〃’▽’〃)
我们知道莫比乌斯函数有一个性质: $\sum\limits_{d|n} \mu(d)=[n=1]$
根据这条性质,我们写出一个类似筛的东西:一个数组,初始都是 $0$。 第 $i$ 轮,将 $i$ 的倍数都加上 $\mu(i)$。
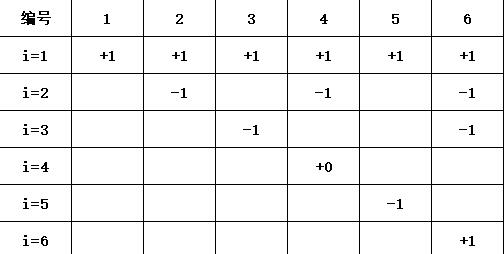
$n$ 轮之后,显然只有第一个位置还剩一个 $1$,其它都变成了 $0$。好好理解下这个表,然后往下看。
那么,假设现在我们要求 $n=1$ 时的答案,但是我们方便求的只有 $n$ 的倍数的答案和,如何转化捏 (⊙.⊙)
我们设 $f(x)$ 表示 $n$ 恰好为 $x$ 的答案,$F(x)$ 表示 $n$ 为 $x$ 的倍数的答案和,即 $\sum\limits_{d|n} f(n)$。
考虑 $\sum\limits_{i=1}^{n} \mu(i)F(i)$,
它 $=\sum\limits_{i=1}^{n}\sum\limits_{i|j} \mu(i)f(j)$
考虑每个 $f(i)$ 被算了多少次,变为:
$\sum\limits_{j=1}^{n} f(j) \sum\limits_{i|j} \mu(i)=\sum\limits_{j=1}^{n} f(j) [j=1]=f(1)$
$f(1)$ 不就是我们要求的,$n$ 恰好为 $1$ 的方案吗(✪ω✪)
其实你也可以联系上面那个表来理解,我们给每一列带上一个 $f(i)$ 的权值,$F(i)$ 就是 $i$ 的倍数列的额。然后我们把所有的 $F(i)*\mu(i)$ 加起来, 根据上面那个表,只会在第一列剩下一个“1”。又因为我们带了一个 $f(i)$ 的权,相当于剩下的就是 $f(1)$ 了。
所以,莫比乌斯容斥的解题步骤:
- 转化成 $n=1$ 的方案(一般这步比较考思维)
- 求 $n$ 的倍数的方案和
说这些有点抽象,还是做点题☆daze~
起飞~
T1. CF 439E
给定 $q$ 个询问,每次给定 $n,k$ ,问有多少种方法,把 $n$ 分成 $k$ 个数相加,并且 所有数 的 $\gcd$ 为 $1$(即:允许有部分的 $\gcd$ 不为 $1$ ,比如 $n=20,k=3$ 时,$\{2,3,15\}$ 是合法的一组拆分)
$q,n\le 10^5,k\le n$
题解
如何转化成上面的 “$n=1$ 的方案数” 呢
设 $f(i)$ 表示:$k$ 个数的 $\gcd=i$ 的方案数,$F(i)$ 表示:$k$ 个数的 $\gcd$ 为 $i$ 的倍数的方案数(即:$k$ 个数都是 $i$ 的倍数的方案数)
$F(i)$ 好求。显然,此时 $i$ 是 $n$ 的因数($k$ 个数都是 $i$ 的倍数,所以它们加起来, $n$ 也是 $i$ 的倍数)。如果不是,那么 $F(i)=0$
然后所有数都是 $i$ 的倍数的划分方案,我们可以把 $i$ 个数并成一块,然后有 $n/i$ 个块,任意划分成 $k$ 个部分,求方案数。然后我们在 $n/i$ 个块中间插入 $n/i-1$ 个隔板,选择 $k-1$ 个,就能把 $n$ 个数分成 $k$ 个部分,每个部分都是 $i$ 的倍数了。这样方案数是 $F(i)=C_{n/i-1}^{k-1}$。预处理阶乘和阶乘逆元,这个 $O(1)$ 算。
然后根据莫比乌斯容斥的式子,$f(1)=\sum\limits_{i=1}^{n} F(i) \mu(i)$。然后在这题中要变下型 (看上面),因为 $i|n$ 时,$F(i)$ 才能按照上面的方法算,否则 $F(i)=0$。于是, $f(1)=\sum\limits_{i|n} F(i)\mu(i)$
然后这个枚举因数是 $O(\sqrt{n})$ 的。总的复杂度 $O(q\sqrt{n})$,能过。
代码 (篇幅问题,我就不放主页了(*^▽^*))(代码看不懂的右下角联系我,或者在代码那边的评论区留言~~❤)
T2. CF 900D
同样是求划分的问题。相当于在 $T1$ 的基础上:
- 去掉 $k$ 的限制
- 一组询问,范围改成 $n\le 10^9$,答案模 $10^9+7$
- 给定了参数 $y$,划分完所有数的 $\gcd=y$ (而不是等于 $1$)
题解
所有数 $\gcd=y$,相当于所有数除以 $y$ 之后 $\gcd=1$。
然后没有了 $k$ 的限制,相当于所有的隔板随便选/不选。这咋整捏 ⊙(・◇・)?
假设有 $n$ 个隔板,答案为 $2^{n}$。然后,$n$ 个数不限个数划分,每个数都是 $y$ 的倍数,方案数就是 $2^{n/y-1}$。
然后要注意的是,$n\le 10^9$,只有一部分 $\mu$ 可以筛出来,超过范围的就只好暴力算了。
这个时间复杂度有点玄学…但还是能过的 φ(>ω<*)
T3. CF1036F
$T$ 组询问,每次询问 $[2,n]$ 中有多少好数。一个数 $x$ 是“好数”,那么不存在任何一个 $k$ 使得 $\sqrt[k]{x}$ 是整数。
$T\le 10^5,x\le 10^{18}$。
题解
一个数是“好数”,那么它分解质因数后,所有指数的 $\gcd=1$
然后我们考虑所有指数的 $\gcd$ 是 $k$ 的倍数怎么算。很显然,这个方案数就是 $\lfloor \sqrt[k]{x} \rfloor$ 。
然后 $k$ 大概枚举到 $60,70$ 就够了。
然后卡亿点点常数就过了 o(╥﹏╥)o
结语
如果您认真的看完并理解了我上面的瞎扯…
恭喜您!学会了莫比乌斯反演!φ(>ω<*)
完结撒花花~~~