算法讲解
其实不用讲,看标题就知道这大概是一个什么样的算法了。
它用来解决这样类型的问题:你要支持,从一个点往一个区间中的所有点连一条边,或者一个区间中的所有点连一条边(有向)。
然后你就要进行一些 最短路/强连通分量/最大流 等图论基本操作了。
那么这个咋整呢(⊙.⊙)
假设我们现在是从第 ⑨ 个点向 $[3,6]$ 区间中的所有点连边。可以如下图处理:
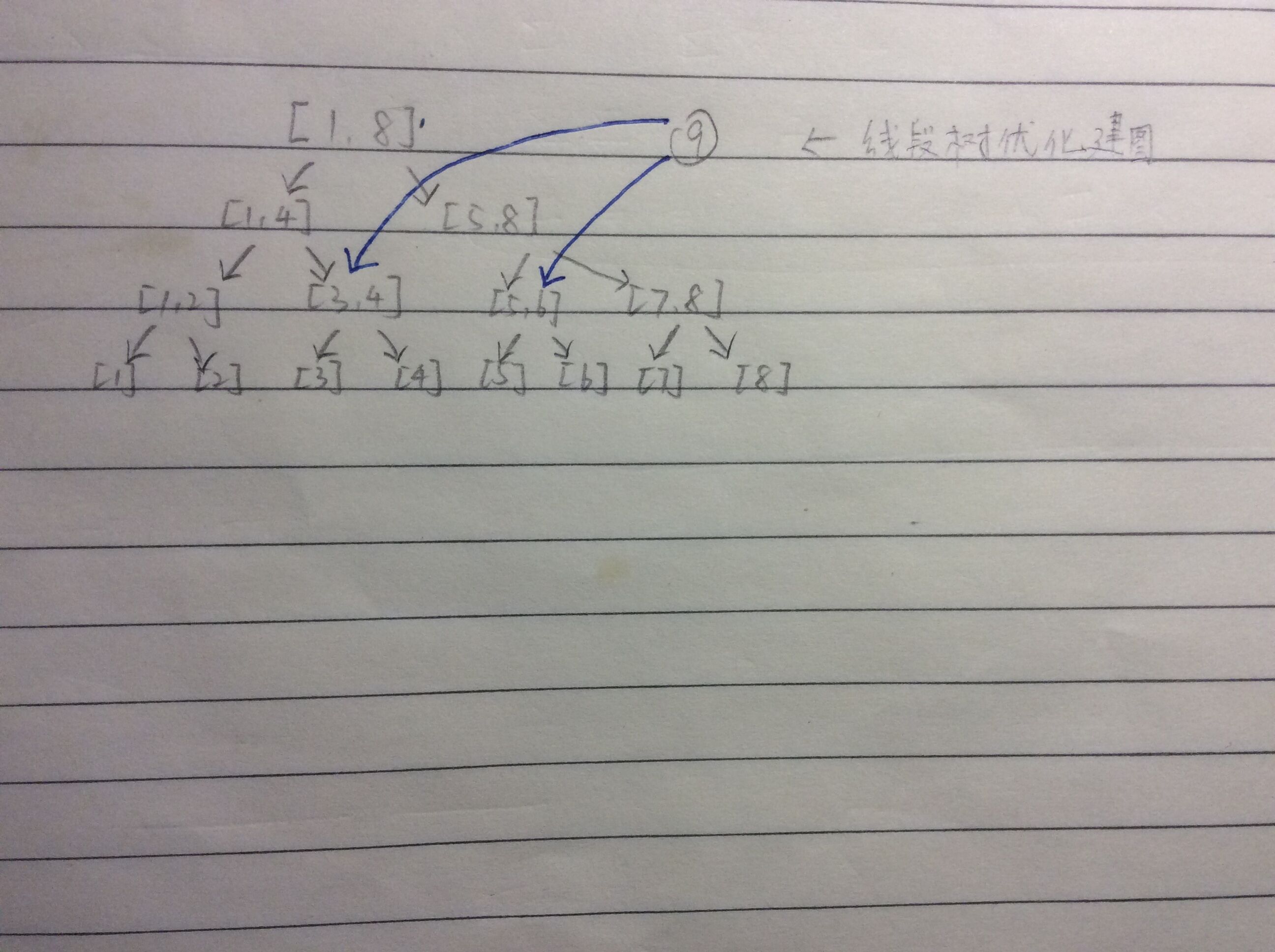
先建一颗线段树,这颗线段树上的每一个非叶子节点都向它的两个儿子连了一条有向边。
接着,我们把 $[3,6]$ 在线段树上拆分一下,变成 $[3,4]+[5,6]$。然后我们从 $9$ 连到线段树节点 $[3,4]$,还有 $[5,6]$,这样就可以 $O(\log n)$ 的时空复杂度实现一次区间连边了,是不是很神奇呢~~(✪ω✪)
(我当时是被这个算法骚到了,吓的我目瞪口呆)
那么这个父子之间的有向边,边权多少呢?首要原则是,不能影响答案,比如你要求最大流,那么影响答案的就是路径最小值,此时要把边权都设置为 $INF$。如果是求最短路,那影响答案的就是路径和,此时把边权设置为 $0$ 就好了 (*^▽^*)
然后我们怎么从区间连向点呢?我们再建一颗树,这颗树的父子边是从儿子到父亲的有向边。然后再把区间拆分一下即可,和上面基本一样,就是反个方向☆daze~
还是那句话(韩信带净化),只有你们想不到,没有出题人出不到,咱们去挑战一把毒瘤例题咯 ~❤
起飞
T1. 超级经典のCF786B Legacy
(诶诶诶别吓我嗷,B 题就 *2600?
(对,没错,这就是 div.1 的神仙,自闭了 o(╥﹏╥)o
这题基本就是板子了(板子也毒瘤的要死),支持 $m$ 个三种形式的连边操作:
- 有向边 $u\xrightarrow[w]{\qquad} v$
- 区间连点 $[l,r]\xrightarrow[w]{\qquad} u$
- 点连区间 $u\xrightarrow[w]{\qquad} [l,r]$
然后给你源点 $S$,求 $S$ 到每个点的最短路。
$n,m\le 10^5,w\le 10^9$,其余所有操作保证有意义且合法
然后,$m$ 指的是连边 操作 的数量,并不代表边数!
(边数可能会到 $O(n^2)$ 级别,存不下
题解
就像上面那样,开两颗线段树,然后连边即可。我们管从父亲到儿子连边的线段树叫“入树”,即 $T_{in}$。它用来存储 $u\xrightarrow[w]{\qquad} [l,r]$ 形式的边。同理,另一颗叫“出树”,即 $T_{out}$。设 $T[l,r]$ 表示线段树 $T$ 上代表区间 $[l,r]$ 的节点。
对于 $u\xrightarrow[w]{\qquad} [l,r]$ 的边,就连边 $T_{out}[u,u]\xrightarrow[w]{\qquad}T_{in}[l,r]$。
同理,对于 $[l,r]\xrightarrow[w]{\qquad} u$ 的边,就连边 $T_{out}[l,r]\xrightarrow[w]{\qquad}T_{in}[u,u]$
还有,两颗线段树对应的叶子节点本质上是同一个 点,所以要连 $n$ 条边权为 $0$ 的无向边,把这些叶子节点合并起来。即,对于每个 $i$,连边 $T_{out}[i,i]\xrightarrow[0]{\qquad}T_{in}[i,i]$
然后从 $T_{out}[s,s]$ 跑一遍最短路即可。最后输出记得输出 $dis[T_{in}[i,i]]$。
注意
刚接触的时候,一定要想清楚 入树 和 出树!
(不建议背,要好好理解,看不懂的私信我
T2. libreoj2255
中文超短题意,我就不概括了。
题解
显然,每个能引爆的所有炸弹,最后是要连续的
对于每个点,向它能一步引爆的炸弹连一条有向边(点到区间连边,这一步用线段树优化)
然后维护它能到的点中,最小和最大的编号即可。这个可以 Tarjan 缩点后一遍 DFS 求出来。
然后就是硬上了…
这题比上面水的是,不用注意出树和入树,这题就一个入树…