exkmp 笔记

发表于 | 阅读次数：
本文字数： 1.4k 字 | 阅读时长 ≈ 6 分钟

exkmp 用于求解这样的问题：

求文本串 $T$ 的每一个后缀与模式串 $M$ 的匹配长度（即最长公共前缀长度）。特别的，取 $M=T$，得到的这个长度被称为 $Z$ 函数。“函数”只是一个叫法，它本质上是个数组…为了好听，后面叫他“$Z$ 数组” （互联网上的确有人这么叫）

符号(字符串)

$|S|$ 表示 $S$ 的长度

$S[l:r]$ 表示 $S$ 从 $l$ 到 $r$ 的子串。如果 $l$ 空着，默认为 $1$；同理 $r$ 默认为 $|S|$。

也就是 $S[:x]$ 表示 $S$ 到 $x$ 结束的前缀，$S[x:]$ 表示 $S$ 从 $x$ 开始的后缀。

$LCP(S_1,S_2)$ 表示 $S_1,S_2$ 的 最长公共前缀 （Longest Common Prefix）

算法讲解

设 $p_i=LCP(T_i,M)$

定义从 $l$ 开始的匹配区间为 $[l,l+p_l-1]$ （设 $l+p_l-1=r$）

我们枚举处理。假设现在已经求好了 $[1,i-1]$ 的 $p$ 数组，要求 $p_i$。记录一个 最靠后 的匹配区间 $[l,r]$ （$l<i$，以 $r$ 靠后为第一关键字，$l$ 靠后为第二关键字），考虑直接从 $[l,r]$ 中继承点答案来，那很显然一个前提就是 $i\le r$ （你 $i$ 在 $r$ 外面继承啥）

显然，$p_i\ge LCP(T[i:r],M)$ （因为 $T[i:r]$ 是 $T[i:]$ 前缀）

由定义， $[l,r]$ 是最长匹配长度，可知 $T[l:r]=M[1:r-l+1]$。

然后现在假如 $l<i\le r$，那么显然 $T[i:r]=M[i-l+1:r-l+1]$

那么 $LCP(T[i:r],M)=LCP(M[i-l+1:r-l+1],M)$

简单想一下，$LCP(A[l:r],A)=min(LCP(A[l:],A),r-l+1)$

我们要求 $[l,r]$ 子串与整个串的 $LCP$，可以先求以 $l$ 开头的整个后缀的与整个串的 $LCP$，然后和区间长度取 $min$。这显然正确。

然后有：

$LCP(M[i-l+1:r-l+1],M)=min(LCP(M[i-l+1:],M),(r-l+1)-(i-l+1+1))$

右边的 $-l+1$ 两个抵消了，就变成 $r-i+1$

然后前面是 $LCP(M[i-l+1:],M)$ 。这不就是 $M$ 的 $Z$ 数组的第 $i-l+1$ 个位置吗！（还记得 $Z$ 数组的定义吗？）

觉得看字母理解不了的看图（自己画的）（纯鼠标）：

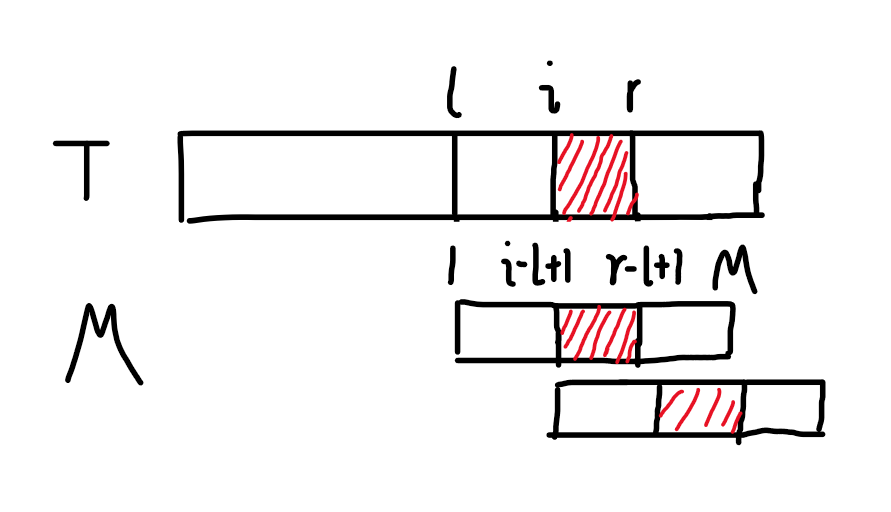
红色的部分就是我们推出来的匹配部分。然后现在我们把 $M$ 移到 $i$ 开头的位置来匹配，就相当于把 $M[i-l+1:r-l+1]$ 这一段（红色）移到 $M$ 的开头处匹配。这一段匹配的长度就是 $min(Z_{i-l+1},r-i+1)$。

假设我们现在能求这个 $Z$ 数组，那么我们已经知道 $p_i$ 的最小值了 ，就是 $min(Z_{i-l+1},r-i+1)$ 。从这个位置开始暴力即可。这样就不用每次从 $1$ 开始匹配了。

求完 $p_i$ 之后，记得用 $[i,i+p_i-1]$ 更新 $[l,r]$。

时间是线性的，我不会证，可以参考网上的证明。

如何求 Z 数组

我们发现 $Z$ 数组就是自己和自己匹配的过程。然后我们把上面过程中 $M$ 换成 $T$ 即可。

所以我们还是记录一个最靠后的匹配区间 $[l,r]$，然后 $p_i$ 就相当于 $Z_i$ 了。

易得：

$Z_i=min(LCP(M[i-l+1:],M),r-i+1)=min(LCP(T[i-l+1:],T),r-i+1)=min(Z_{i-l+1},r-i+1)$

求完 $Z_i$ 之后，记得用 $[i,i+Z_i-1]$ 来更新 $[l,r]$。

一样，也是从这里开始暴力即可。时间复杂度依然是线性的，可以参考网上的证明。

模板

洛谷板子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
using namespace std;
#define N 20000007
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.Start(u),v=G.To(i);~i;i=G.Next(i),v=G.To(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define Flandre_Scarlet int
#define IsMyWife main
char _c;
int I()
{
    int x=0; int f=1;
    while(_c<'0' or _c>'9') f=(_c=='-')?-1:1,_c=getchar();
    while(_c>='0' and _c<='9') x=(x<<1)+(x<<3)+(_c^48),_c=getchar();
    return (x=(f==1)?x:-x);
}
void Rd(int cnt,...)
{
    va_list args; va_start(args,cnt);
    F(i,1,cnt) {int* x=va_arg(args,int*);(*x)=I();}
    va_end(args);
}

char a[N],b[N];
void Input()
{
	scanf("%s%s",a+1,b+1);
}
int z[N];
void Z(char s[]) // 求 Z 函数
{
	int n=strlen(s+1);
	z[1]=n; F(i,2,n) z[i]=0;
    // Z[1]=n 特判，同时也是递推边界
	int l=0,r=0;
	F(i,2,n) 
	{
		if (i<=r) z[i]=min(z[i-l+1],r-i+1); // 推理出下界
		while(i+z[i]<=n and s[i+z[i]]==s[z[i]+1]) ++z[i]; // 暴力
		if (i+z[i]-1>=r) l=i,r=i+z[i]-1; // 更新最靠后的匹配位置
	}
}
int p[N];
void ExKmp(char s[],char t[])
{
	int n=strlen(s+1);
	Z(t);
	int l=0,r=0;
	F(i,1,n)
	{
		if (i<=r) p[i]=min(z[i-l+1],r-i+1); // 推理出下界
		while(i+p[i]<=n and s[i+p[i]]==t[p[i]+1]) ++p[i]; // 暴力
		if (i+p[i]-1>r) l=i,r=i+p[i]-1; // 更新最靠后的匹配位置
	}
}
void Soviet()
{
	ExKmp(a,b);
	int n=strlen(a+1),m=strlen(b+1);
	long long ans=0;
	F(i,1,m) ans^=1ll*i*(z[i]+1);
	printf("%lld\n",ans);
	ans=0;
	F(i,1,n) ans^=1ll*i*(p[i]+1);
	printf("%lld\n",ans);
}
Flandre_Scarlet IsMyWife()
{
	Input();
	Soviet();
	getchar();
	return 0;
}
w